การวิเคราะห์ข้อมูล (Data analytics) หมายถึง การจัดการข้อมูลด้วยวิธีต่าง ๆ เช่น การคำนวณ การนำเสนอข้อมูล เพื่อให้ได้ผลลัพธ์ตามวัตถุประสงค์ การวิเคราะห์เป็นการแยกแยะสิ่งที่จะพิจารณาออกเป็นส่วนย่อยที่มีความสัมพันธ์กัน เพื่อทำความเข้าใจแต่ละส่วนให้
แจ่มแจ้ง รวมทั้งการสืบค้นความสัมพันธ์ของส่วนต่าง ๆ เพื่อดูว่าส่วนประกอบปลีกย่อยนั้นสามารถเข้ากันได้หรือไม่ สัมพันธ์เกี่ยวเนื่องกันอย่างไร ซึ่งจะช่วยให้เกิดความเข้าใจต่อสิ่งหนึ่งสิ่งใดอย่างแท้จริง
การวิเคราะห์เชิงพรรณนา (Descriptive analytics) เป็นรูปแบบพื้นฐานของการวิเคราะห์ข้อมูลเพื่ออธิบายลักษณะของข้อมูลที่เก็บรวบรวม โดยใช้การคำนวณทางคณิตศาสตร์และสถิติพื้นฐาน เช่น การหาสัดส่วนหรือร้อยละ การวัดค่ากลางของข้อมูล การวัดการกระจายของข้อมูล และการหาความสัมพันธ์ของชุดข้อมูล การวิเคราะห์ประเภทนี้จึงเป็นรูปแบบที่นำมาใช้งานเพื่อดูภาพรวมของข้อมูลที่สนใจ
1. การหาสัดส่วนหรือร้อยละ
การหาสัดส่วนหรือร้อยละ เป็นการจัดการข้อมูลที่ซ้ำกันให้เป็นระเบียบและเป็นหมวดหมู่ ซึ่งจะทำให้ง่ายต่อการนำข้อมูลไปใช้ และง่ายต่อการสังเกตการเปลี่ยนแปลงต่าง ๆ ที่เกิดขึ้น โดยอาจแสดงในรูปของเศษส่วน ทศนิยม หรือร้อยละ และสามารถนำเสนอในรูปของแผนภูมิ หรือแผนภาพ เพื่ออธิบายความหมายของข้อมูลชุดนั้น เช่น เช่น จำนวนนักเรียนชาย-หญิง ในห้องเรียน แสดงผลเป็นร้อยละต่อจำนวนนักเรียนทั้ง
ห้อง
การหาสัดส่วน (Proportion) คือ ความสัมพันธ์ของจำนวนย่อยกับจำนวนรวมทั้งหมด กล่าวคือ ให้ถือจำนวนรวมทั้งหมดเป็น 1 ส่วน เช่น ในการสำรวจคนในหมู่บ้านหนึ่งจำนวน 800 คน เป็นหญิง 300 คน เป็นชาย 500 คน
ร้อยละหรือเปอร์เซนต์ (Percentage or Percent) คือ สัดส่วนเมื่อเทียบต่อ 100 การคำนวณก็ทำได้ง่าย โดยเอา 100 ไปคูณสัดส่วนที่ต้องการหาผลลัพธ์ก็จะออกมาเป็นร้อยละหรือเปอร์เซนต์
2. การวัดค่ากลางของข้อมูล
การวัดค่ากลางของข้อมูล ใช้เพื่อหาค่าที่เป็นตัวแทนของข้อมูลทั้งหมด ทำให้สะดวกในการจดจำ หรือ สรุปเรื่องราวเกี่ยวกับข้อมูลชุดนั้น ๆ ได้มากขึ้น ค่กลางของข้อมูลที่นิยมใช้ ได้แก่ ค่าเฉลี่ย (Mean) มัธยฐาน (Median) และฐานนิยม (Mode) สำหรับชุดข้อมูลเชิงปริมาณที่มีค่าใกล้เคียงกัน (ค่าการกระจายของข้อมูลต่ำ) ค่าเฉลี่ยอาจเป็นค่ากลางที่ดี แต่ค่าเฉลี่ยอาจไม่เหมาะที่จะใช้เป็นค่ากลางของชุดข้อมูลที่มีค่าแตกต่างกันมาก
คือมีข้อมูลบางตัวที่ค่าสูงมาก ๆ หรือต่ำมาก ๆ ดังนั้นการพิจารณาค่าเฉลี่ยจึงควรจะพิจารณาการกระจายของ ข้อมูลด้วย ซึ่งสามารถดูได้จากค่าส่วนเบี่ยงเบนมาตรฐาน (Standard deviation)
2.1 ค่าเฉลี่ย (Mean)
ค่าเฉลี่ย (Mean) คือ ค่าที่ได้จากการเฉลี่ยข้อมูลที่สนใจทั้งหมด โดยคำนวณจากผลรวมของ ข้อมูลที่สนใจทั้งหมดหารด้วยจำนวนข้อมูล ถ้าให้ X1, X2, Xn…. เป็นข้อมูล N จำนวนประชากร หรือใช้ X1, X2, X3, Xn, เป็นข้อมูลเพียง n จำนวนจากกลุ่มตัวอย่าง
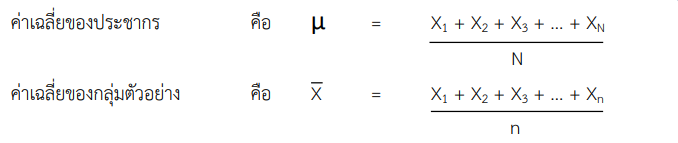
ซึ่งค่าเฉลี่ยมีความเหมาะสมในการนำมาใช้เป็นค่ากลางของข้อมูล เมื่อข้อมูลนั้น ๆ ไม่มีค่าใดสูงหรือต่ำกว่าค่าที่เหลืออื่นอย่างผิดปก เช่น หากต้องการหาค่าเฉลี่ยของอายุลูกค้าจากข้อมูลที่ได้จากขั้นตอนการเตรียมข้อมูล เพื่อนำอายุเฉลี่ยไปวิเคราะห์หากลุ่มลูกค้าเป้าหมาย
2.2 มัธยฐาน (Median)
มัธยฐาน (Median) คือ ค่าที่อยู่ในตำแหน่งกึ่งกลางของข้อมูลทั้งหมด เมื่อนำข้อมูลดังกล่าวมาเรียงจากค่าน้อยไปหาค่ามาก

2.3 ฐานนิยม (Mode)
ฐานนิยม (Mode) คือ ค่าของข้อมูลที่มีความถี่สูงสุดหรือค่าที่ซ้ำกันมากที่สึดจากข้อมูลทั้งหมดโดยฐานนิยมป็นข้อมูลที่เหมาะสมในการนำมาเป็นค่กลางของข้อมูลที่เป็นมาตรฐานต่าง ๆ เช่น ขนาดของเสื้อผ้า ขนาดยางรถยนต์ ข้อมูลที่มีการแจกแจงความถี่แล้ว สามารถจำแนกวิธีการหาค่าฐานนิยมได้ ดังนี้
(1) ข้อมูลที่ได้รับเป็นค่าที่ได้จากการสังเกตแต่ละค่า ค่าฐานนิยมมีได้สูงสุดเพียง 2 ค่าเท่านั้น ถ้าข้อมูลชุดใดมีข้อมูลที่ซ้ำกันมากที่สุดเท่ากันมากกว่า 2 ค่า ถือว่าข้อมูลชุดนั้นไม่มีค่ฐานนิยม เช่น หากต้องการหาค่าฐานนิยมของอายุลูกค้าจากข้อมูลที่ได้จากขั้นตอนการเตรียมข้อมูล เพื่อนำไป
วิเคราะห์หากลุ่มลูกเค้าเป้าหมาย สามารถทำได้ ดังนี้
1. ข้อมูลอายุของลูกค้ามีจำนวน 7 ข้อมูล ดังนี้ 24, 25, 28, 29, 32, 32, 40
2. ข้อมูลที่มีความถี่มากที่สุด คือ 32
3. ค่าฐานนิยม คือ ข้อมูลอายุ 32 ปี
2.4 ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation)
ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation) คือ ค่าที่ใช้บอกการกระจายข้อมูลที่ได้จากการหารากที่สองของผลรวมข้อมูลที่เป็นผลต่างกำลังสองระหว่างค่ของข้อมูลแต่ละตัวกับค่าเฉลี่ย แล้วหารด้วยจำนวนข้อมูล
ส่วนเบี่ยงเบนมาตรฐานที่ใช้ในการวัดการกระจายของชุดข้อมูล จะมีค่าเป็นบวกเสมอ และมีหน่วยเดียวกับค่าของข้อมูล ถ้าส่วนเบี่ยงเบนมาตรฐานมีค่าน้อยหรือใกล้ศูนย์ หมายถึง ข้อมูลมีการกระจายน้อยมากหรือข้อมูลเกาะกลุ่มกัน แต่ถ้าส่วนเบี่ยงเบนมาตรฐานมีค่ามาก จะหมายถึงข้อมูลมีการกระจายมากหรือข้อมูลมีความแตกต่างกันมากนั่นเอง นักสถิตินิยมใช้ค่าส่วนเบี่ยงเบนมาตรฐานนี้ในการวัดการกระจาย เนื่องจากมีการ
ใช้ข้อมูลทุก ค่า หรือมีการนำข้อมูลทุกตัวมาคำนวณ ซึ่งจะทำให้คำการกระจายมีความละเอียดถูกต้อง และเชื่อถือได้

3. การหาความสัมพันธ์ของชุดข้อมูล
การหาความสัมพันธ์ของชุดข้อมูลการวิเคราะห์ความสัมพันธ์เชิงเส้นระหว่างข้อมูล 2 ชุด (Pairwvise) จะบ่งบอกถึงทิศทาง (Direction)
ของความสัมพันธ์ ทิศทางของความสัมพันธ์สามารถพิจารณาได้ 2 กรณี คือ
ความสัมพันธ์เชิงบวก หมายความว่า สิ่งที่สนใจทั้งสองสิ่งมีการเพิ่มขึ้นหรือลดลงไปใน ทิศทางเดียวกัน เช่น ค่าของ X เพิ่มขึ้น 1 ค่าของ Y จะเพิ่มขึ้น 1
ความสัมพันธ์เชิงลบ หมายความว่า สิ่งที่สนใจทั้งสองสิ่งมีการเพิ่มขึ้นหรือลดลงไปใน ทิศทางตรงกัน ข้าม เช่น ค่าของ X เพิ่มขึ้น 1 ค่าของ Y กลับลดลง 1
การวิเคราะห์ความสัมพันธ์เบื้องตันสามารถทำได้โดยนำคำของข้อมูลทั้งสองชุดมาสร้างแผนภาพการกระจาย ซึ่งทำให้เป็นทิศทางของความสัมพันธ์ได้ชัดเจน และสามารถประมาณระดับความสัมพันธ์ได้
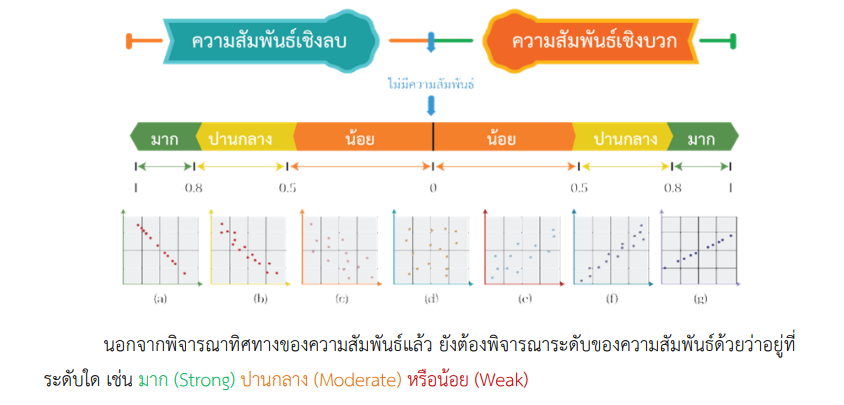
ข้อควรระวัง ในการภิปรายผลของการวิเคราะห์ความสัมพันธ์ คือ ค่าความสัมพันธ์ที่ได้สามารถบอกได้เพียงว่า ข้อมูลทั้งสองชุดมีความสัมพันธ์กันหรือไม่ มีทิศทางความสัมพันธ์เป็นแบบใด และมีระดับความสัมพันธ์มากหรือน้อยเพียงใดแต่ไม่สามารถสรุปว่าข้อมูลชุดหนึ่งส่งผลต่อการเปลี่ยนแปลงค่าของข้อมูลอีกชุดหนึ่ง โดยความสัมพันธ์นั้น อาจมาจากสาเหตุเดียวกัน เช่น หากเกิดภัยแล้งแล้วทำให้จำนวนม้าลายและวัวป่าลด
ลงพร้อมกัน ด้วยเหตุนี้เราจึงไม่สามารถสรุปได้ว่าการลดลงของจำนวนวัวป่าส่งผลต่อการลดลงของจำนวนม้าลาย เนื่องจากอาจมีปัจจัยอื่นเข้ามา
เกี่ยวข้องด้วยนอกจากนี้ จากความสัมพันธ์ข้างต้น เราสามารถประมาณจำนวนของม้าลายจากจำนวนของวัวป่าได้ อีกทั้งยังสามารถทำนายจำนวนของวัวป่าและม้าลายในอนาคตได้ด้วยข้อมูลที่มีอยู่ในปัจจุบัน โดยใช้การวิเคราะห์ชิงทำนาย ซึ่งจะกล่าวถึงในหัวข้อต่อไป



